今回は、京都大学の空間ベクトルの問題を最強の解法を使って解説していきます。
実は以前に【基礎編】をアップしてます。(宣伝すいません笑)
基礎編では、平面&空間ベクトルの問題を解くときに用いる4つの条件と、機械的に問題を解くことができる最強の解法パターンについて、演習問題を通して詳しく解説しています。
特に「共線条件」と「共面条件」がよくわかっていないという方や、ベクトルの問題が難しいと感じている方は、ぜひ読んでみてください!
また、本問題を解いてから解説を見たいという方は、【基礎編】にも本問題を載せていますのでそちらを参考に解いてみてください!
【基礎編】から見ていただくと、学習効果が跳ね上がりますよ!!

それでは早速解説していきます。
演習問題の解説
【課題】京都大
座標空間に4点 A(2,1,0) , B(1,0,1) , C(0,1,2) , D(1,3,7)がある。
3点A,B,Cを通る平面に関して点Dと対称な点をEとするとき、点Eの座標を求めよ。
こちらが解説する問題です。
基礎編で習得した最強の解法を使って解いていきます。
まずは図を書いて状況を整理しましょう。
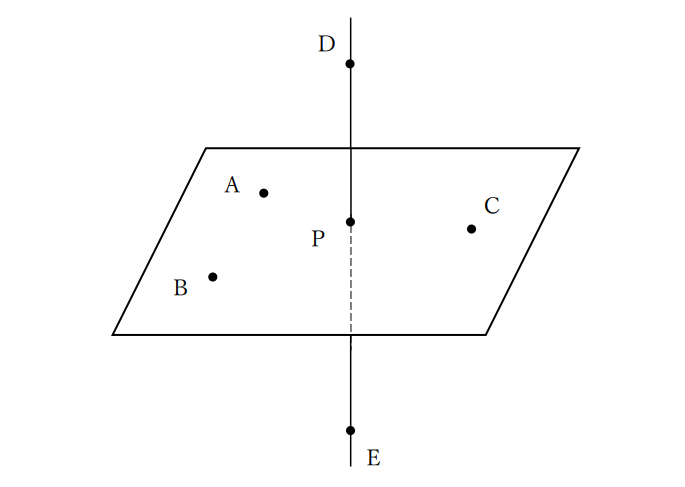
この問題のポイントは、平面ABC上に、平面ABCに対して直線DFが垂直に交わるような点Pを設定することにあります。
かなり想像力が問われる問題だね・・・。
この設定を思いつくまでに、まず座標が与えられている(ベクトルの成分として利用できる) ことから、この問題を空間ベクトルの知識で解くことを決め、垂直条件と共面条件を余すことなく使えるように設定ができないかを考えてみた、というプロセスを踏んでいます。
多く問題を解けば、誰でもこのような思考プロセスを踏めるようになると思います。
諦めずに頑張ってくださいね!
ということで、こちらで設定した点Pの座標をP(p,q,r)と置きましょう。
そして、問題を解く上で使えそうなベクトルの成分を求めます。
$$\overrightarrow{AB}=(-1,-1,1)$$ $$\overrightarrow{AC}=(-2,0,2)$$ $$\overrightarrow{AP}=(p-2,q-1,r)$$ $$\overrightarrow{DP}=(p-1,q-3,r-7)$$
ここからは魔法の解法を使っていきます。
魔法の解法とは、次の4つの条件を上から順に当てはめていくというものでしたね。
- 平行条件
- 垂直条件 ⇔ 内積0
- 共線条件 ⇔ 3点が同一直線上にある
- 共面条件 ⇔ 4点が同一平面上にある
まずは平行条件から見ていきましょう。
平行なベクトルは見当たらないね。
次に垂直条件を見てきましょう。
\(\overrightarrow{DP}\)が\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)に対して垂直だ!
そう、この条件が使いたくて設定したんでしたよね!
垂直条件は言い換えれば内積0条件です。
早速、立式していきましょう!
$$\vec{DH}\cdot\vec{AB}=0$$
先ほど求めた成分を代入し、整理すると、
$$p+q-r=-3 -①$$
同様に、\(\vec{DH}\cdot\vec{AC}=0\)より
$$p-r=-6 -②$$
垂直条件から以上の2式を得ます。
続いて、共線条件を見ていきましょう。
3点D,P,Eが同一直線状にあるよ!
ただし!このことは共線条件でわざわざ表す必要はないですよね。
なぜなら点Eは点Dに対して対称な点だからです。
すなわち設定した点Pまでの距離が等しいんです。
立式するならば、
$$\overrightarrow{DP}=\overrightarrow{PE} -(*)$$
といったところでしょうか。
これは点Eの座標を求める決定打になりそうですね。
これはとりあえず今は置いておきましょう。
では最後に共面条件を見ていきましょう。
点Pが平面ABC上に存在してる!
ここから、この平面において求める\(\overrightarrow{AP}\)は、\(\overrightarrow{AB}\)を実数倍(ここでは実数をsとする)したものと、\(\overrightarrow{AC}\)を実数倍(ここでは実数をtとする)したものを図的に足したものと考えることができるんでしたよね!
イメージはこんな感じです。
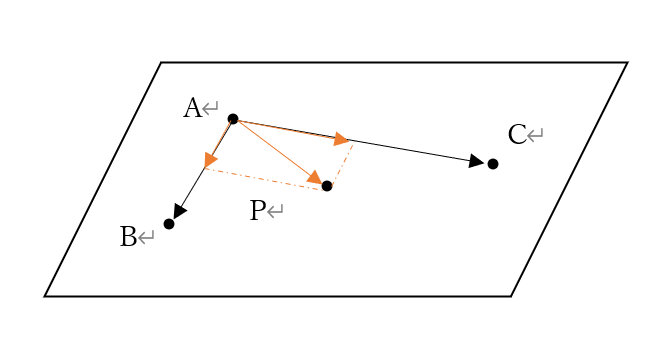
ベクトルの和は、始点を合わせて平行四辺形を作るんだったね!
これらをもとに立式すると次のようになります。
$$\overrightarrow{AP}=\it{s}\overrightarrow{AB}+\it{t}\overrightarrow{AC}$$
ここに、始めに求めておいた成分たちを代入し、各成分ごとで式を立てると、
\begin{cases} p – 2 = -s – 2t -③\\ q – 1 = -s -④ \\ r = s + 2t -⑤ \end{cases}という式を得ることができます。
これで、未知数5つに対して式が5本立ったので、後は連立すれば未知数が求まります。
式を解くには、基本的に未知数の個数分の式が必要だよ!
したがって①~⑤の連立方程式を解くことで、
$$p=-2 , q=3 , r=4 , s=-2 , t=3$$
と未知数を得ます。
これによって点Pの座標がP(-2,3,4)であることがわかりました。
さて、いよいよ求める点Eの座標をE(x,y,z)と置きましょう。
共線条件のときに立てた(*)式に、先ほど求めた点Pの成分も代入して、
$$(-3,0,-3)=(x+2,y-3,z-4)$$
後は成分ごとで連立方程式を立てて解けば、
$$(x,y,z)=(-5,3,1)$$
となります。
以上より求める点Eの座標はE(-5,3,1)となり、試合終了です!
終わりに
お疲れ様でした!
今回は、基礎編で学んだ解法を使って京都大学の過去問を解説してみました。
皆さん、いかがだったでしょうか?
何度も言いますが、ベクトルはパターンで解くことができます。
4つの条件を十分に理解し、使いこなしていきましょう!
今後も数学に関する記事も少しずつ書いていく予定です。
苦手なジャンルがあればぜひ、お問い合わせフォームなどを活用して質問してくださいね。
楽しみに待っています!
以上、せりくんでした。またね。