はじめまして!四国で理系大学生をしています。せりくんです。
よろしくおねがいします!
今回は、平面&空間ベクトルの頻出問題を機械的に解くことができるシステマチックな解法を、演習問題を通して皆さんに伝授したいと思います!
このやり方を覚えてしまえば、ベクトル範囲の問題の7割程度は解けます。
まさに最強の解法です!!
なお、ここで「7割」とした理由は次の系統の問題には対応していないためです。
- 基本的なベクトルの演算
- 平面上の点の存在範囲に関する問題
- 円などのベクトル方程式の問題
これらの問題にも典型的な解法があります。またご紹介させてください。
では早速、本題に入っていきましょう!
【平面ベクトル】いつも心に3つの条件
まず、平面ベクトルの問題に用いる3つの条件について理解しましょう!
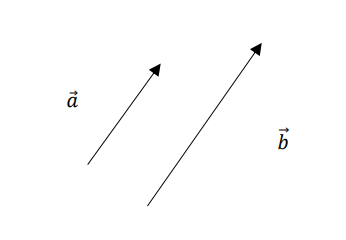
1.平行条件
⇔ 0でない2つのベクトルが平行であるなら、片方のベクトルは、もう片方のベクトルの実数倍で表せる。
$$\vec{b}=\it{k}\vec{a}$$
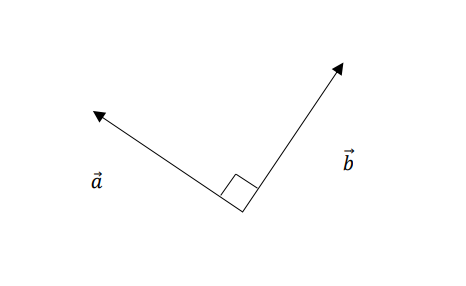
2.垂直条件
⇔ 2つのベクトルが直行している場合、その内積が0。
$$\boldsymbol{a} \cdot \boldsymbol{b} =0$$
3.共線条件
⇔ 3点が同一直線状にある。
\begin{eqnarray} \overrightarrow{AP}&=&\it{t}\overrightarrow{AB}\\ \overrightarrow{OP}-\overrightarrow{OA}&=&\it{t}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)\\ \overrightarrow{OP}&=&\it\left({1-t }\right)\overrightarrow{OA}+\it{t}\overrightarrow{OB} \end{eqnarray}これだけではわかりにくいので、図を用いて補足します。

この図にある\(\overrightarrow{OP}\)を求める場合、まず\(\overrightarrow{AP}\)が\(\overrightarrow{AB}\)の実数倍(ここでは\(t\)倍とする)で書けることに注目して式を立てます。
$$\overrightarrow{AP}=\it{t}\overrightarrow{AB}$$
この後、始点を揃えます。(今回は始点を\(O\)に揃えます。)
ベクトルの始点揃えは「後-前」でしたね!
$$\overrightarrow{OP}-\overrightarrow{OA}=\it{t}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)$$
後は展開して、左辺に求める\(\overrightarrow{OP}\)が来るように整理します。
$$\overrightarrow{OP}=\it\left({1-t}\right)\overrightarrow{OA}+\it{t}\overrightarrow{OB}$$
ここから\(\left({1-t }\right)\)=\(s\)と置くことで、
\begin{eqnarray} \overrightarrow{OP}&=&\it{s}\overrightarrow{OA}+\it{t}\overrightarrow{OB}\\ (\it{s}+\it{t}&=&1) \end{eqnarray}とすることもできます。
なんだか見覚えのある形になったね!
どちらを使ってもいいですが文字が増えるのを避けるために、\(\left({1-t }\right)\)=\(s\)で置かない方を個人的におすすめします。
以上、これが3つの条件です。
”いつも心に3つの条件”と覚えよう!
そして、伝授する解法は
「3つの条件を上から順に当てはめていく」
ただそれだけです。
これによって得られた式から未知数を求め、答えを導きます。
とは言っても、この説明だけではわかりにくいですよね笑
何事も「習うより慣れろ」です!
次は平面ベクトルの頻出問題を使って、この解法の威力を確認していきましょう。
【平面ベクトル】演習問題
三角形ABCにおいて、辺ABを4:3に内分する点をD、辺ACを3:1に内分する点をEとする。また、線分BEと線分CDの交点をFとし、直線AFと辺BCの交点をGとする。
問. BF:FEを求めよ。 (徳島大2012改題)
まずは図を書いて状況を整理しましょう。
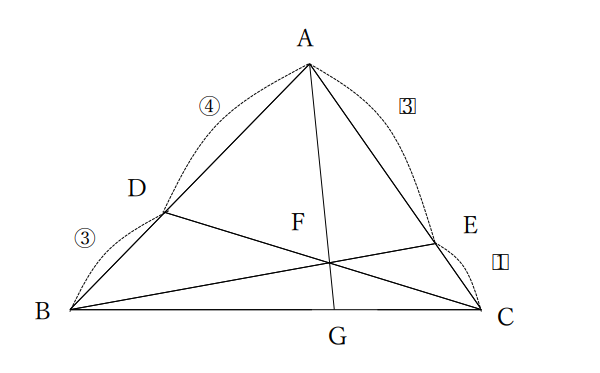
図を書くとこんな感じになりますね。
この手の問題はセンター試験や私立大の入試でよく出ますが、\(\overrightarrow{AF}\)を求めるやり方で必ず解くことができます。
はじめに、問題からわかる情報をメモしておきます。
$$\overrightarrow{AD}=\frac{4}{7}\overrightarrow{AB}$$ $$\overrightarrow{AE}=\frac{3}{4}\overrightarrow{AC}$$
これで準備完了です。
では早速3つの条件を上から順に当てはめていきましょう。
まずは平行条件から。
どこにも平行なところはないね。
このように条件に当てはまらない場合は式を立てることができませんが、他の条件で式が立つので大丈夫です。
次に垂直条件です。
これも無いね~。
この2つは使えることは少ないので、出てきたらラッキー程度に思ってもらえば大丈夫です。
最後に共線条件を見ていきましょう。
これは何箇所かありそうだね!
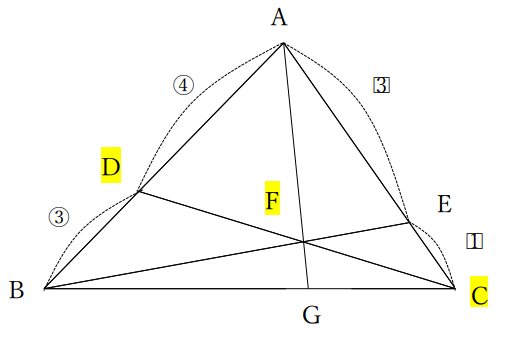
今回は\(\overrightarrow{AF}\)を求めたいので、点Fを含んでいることが重要です。
点Fを含んで、3点が同一直線状にある箇所に色を付けてみました!
これについて、まず\(\overrightarrow{DF}\)が\(\overrightarrow{DC}\)の実数倍(ここでは\(t\)倍とする)で書けることに注目して式を立てましょう。
$$\overrightarrow{DF}=\it{t}\overrightarrow{DC}$$
ここから始点を\(A\)に揃えます。「後-前」ですね。
$$\overrightarrow{AF}-\overrightarrow{AB}=\it{t}\left(\overrightarrow{AC}-\overrightarrow{AD}\right)$$
次に、求めたい\(\overrightarrow{AF}\)について整理します。
$$\overrightarrow{AF}=\it\left({1-t}\right)\overrightarrow{AD}+\it{t}\overrightarrow{AC}$$
最後に先程準備しておいた\(\overrightarrow{AD}=\frac{4}{7}\overrightarrow{AB}\)を代入して、
$$\overrightarrow{AF}=\frac{4}{7}\it\left({1-t}\right)\overrightarrow{AB}+\it{t}\overrightarrow{AC}$$
を得ます。
さて、点Fを含んでいて3点が同一直線状にある箇所がもう一つありますね。
再度、図で確認しましょう。
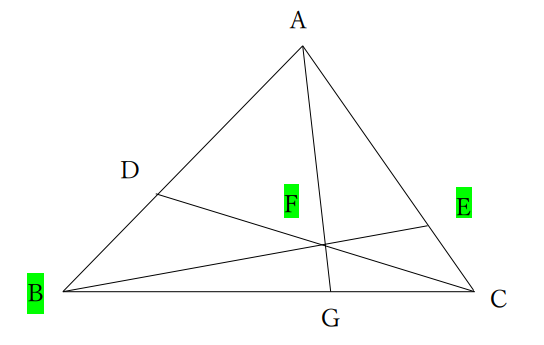
そう、この3点ですね。
早速、\(\overrightarrow{BF}\)が\(\overrightarrow{BE}\)の実数倍(ここでは\(s\)倍とする)で書けることに注目して式を立てましょう。
$$\overrightarrow{BF}=\it{s}\overrightarrow{BE}$$
ここからも同様の手順で、求めたい\(\overrightarrow{AF}\)について整理していくと、
$$\overrightarrow{AF}=\it\left({1-s}\right)\overrightarrow{AB}+\frac{3}{4} \it{s}\overrightarrow{AC}$$
が得られます。
求めたい\(\overrightarrow{AF}\)についての式が2つ立ったので、係数比較をします。
このとき、係数比較するベクトルが一次独立であることを必ず言っておきましょう。
この文言が無いと減点されます。
$$\overrightarrow{AB}\neq\overrightarrow{AC}$$ $$\overrightarrow{AB}\neq0$$ $$\overrightarrow{AC}\neq0$$
よって、\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)は一次独立。
後は係数比較して、
$$\it{s}=\frac{3}{4}$$ $$\it{t}=\frac{9}{16}$$
を得ます。
ここまで来たら大丈夫ですね。
求めたいのはBF:FEですので、関係するベクトルは
$$\overrightarrow{BF}=\it{s}\overrightarrow{BE}$$
求めたsを代入して、
$$\overrightarrow{BF}=\frac{3}{4}\overrightarrow{BE}$$
図と照らして考えれば、BF:FE=3:1 と答えが求まります。
計算はキツイけど、機械的に解けるね!
以上で演習を終わります。お疲れ様でした!
さて、平面ベクトルにおける3つの条件を用いた解法を理解していただけたでしょうか?
簡単におさらいをすると、
「3つの条件を上から順番に当てはめていき、式を立てて計算する」
でしたね!
この解法は非常に汎用性が高いんです。
なんと、空間ベクトルの問題も全く同じ解法で解くことができます!
ただし、空間ベクトルではここで使用した3つの条件に加えて、もう1つ条件を付け足す必要があることに注意が必要です。
次に、その条件について説明します。
【空間ベクトル】共面条件
空間ベクトルの問題を解く際には、先程説明した3つの条件に加えて「共面条件」という条件が必要になります。
言い換えれば、「4点が同一平面上にある」という条件です。
こちらも図を用いて理解していきましょう。
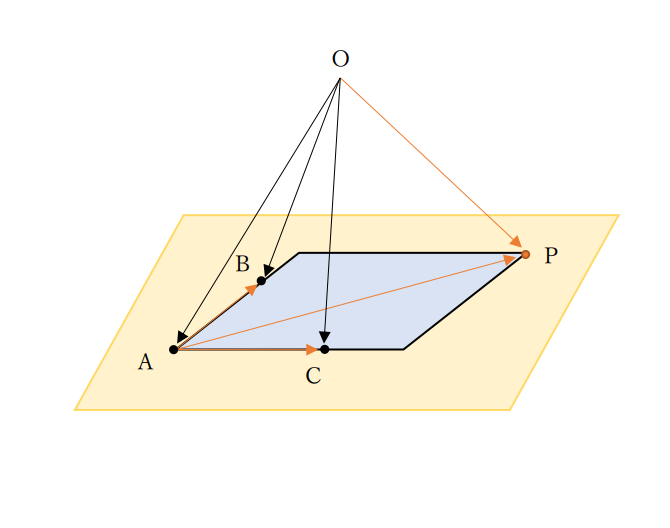
共線条件と同様に、\(\overrightarrow{AP}\)を求めることにします。
この図から、点Pが点A,B,Cと同一平面上(黄色の平面)にあることがわかりますね。
そしてこの平面において求める\(\overrightarrow{AP}\)は、\(\overrightarrow{AB}\)を実数倍(ここでは実数をsとする)したものと、\(\overrightarrow{AC}\)を実数倍(ここでは実数をtとする)を図的に足したものと理解できます。
イメージはこんな感じ。
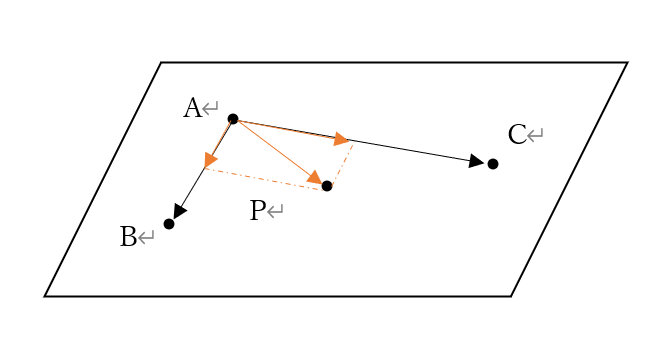
ベクトルの和は、始点を合わせて平行四辺形を作るんだったね!
これを式にするとこんな感じ。
$$\overrightarrow{AP}=\it{s}\overrightarrow{AB}+\it{t}\overrightarrow{AC}$$
そして、この式が共面条件のスタートの式となります。
また、共線条件のときと同様に始点を変更すれば見覚えのある形にも変形できます。
ということで、先程の式の始点をAからOに変更して\(\overrightarrow{OP}\)を求めることにしましょう。
$$\overrightarrow{OP}-\overrightarrow{OA}=\it{s}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)+\it{t}\left(\overrightarrow{OC}-\overrightarrow{OA}\right)$$
後は展開して、左辺に求める\(\overrightarrow{OP}\)が来るように整理します。
$$\overrightarrow{OP}=\it\left({1-s-t}\right)\overrightarrow{OA}+\it{s}\overrightarrow{OB}+\it{t}\overrightarrow{OC}$$
この形も見覚えがあるね!
ここからさらに\(\left({1-s-t }\right)\)=uと置くことで
\begin{eqnarray} \overrightarrow{OP}&=&\it{u}\overrightarrow{OA}+\it{s}\overrightarrow{OB}+it{t}\overrightarrow{OC}\\ (\it{u}+\it{s}+\it{t}&=&1) \end{eqnarray}ともできますので、お好みで使い分けてください。
オススメはuと置かない方ですが、計算が煩雑になります。
共線・共面条件は、何も見ずに自分で導出ができるようになるまで練習を重ねてくださいね!
【空間ベクトル】いつも心に4つの条件
前述した通り、空間ベクトルと平面ベクトルの解法は同じです。
平面ベクトルを解く際に使用した3つの条件に共面条件を加えた4つの条件を上から順に当てはめていくだけです。
ここで改めて、4つの条件を整理したいと思います。
- 平行条件
- 垂直条件 ⇔ 内積0
- 共線条件 ⇔ 3点が同一直線上にある
- 共面条件 ⇔ 4点が同一平面上にある
空間ベクトルでは”いつも心に4つの条件”で覚えよう!
では、この条件を心にとめて演習問題に挑戦していきましょう!
ただし、計算は省略しますので各自で頑張ってくださいね。
【空間ベクトル】演習問題

まずは図を書いて状況を整理しましょう。
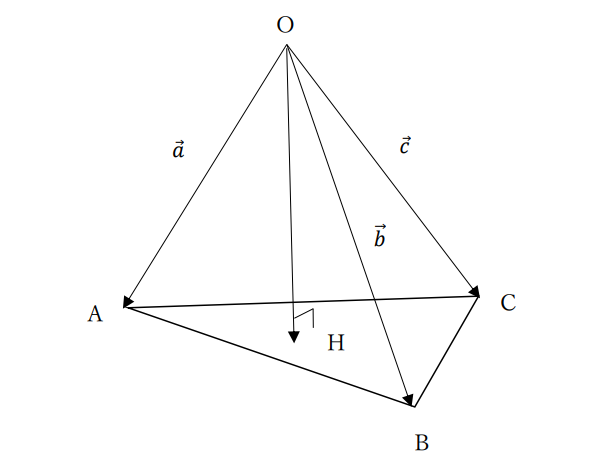
状況をイメージできましたか?
では早速、4つの条件を上から順に当てはめていきましょう!
まずは平行条件です。
どこにも平行なベクトルはないよ。
こういう場合は、式を立てれないので次の条件にいくんでしたね。
では続いて、垂直条件です。
\(\overrightarrow{OH}\)が\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)に対して垂直だ!
これらを式にしてみると、以下のようになります。
$$\vec{OH}\cdot\vec{AB}=0$$
$$\vec{OH}\cdot\vec{AC}=0$$
これらは後々使うので置いておきましょう。
次は共線条件ですが、3点が同一直線上にある箇所はありませんね。
ということで、最後に共面条件を見ていきましょう。
点Hが平面ABC上に存在してる!!
これは大きい情報ですね!
この平面において\(\overrightarrow{AH}\)は\(\overrightarrow{AB}\)を実数倍したものと、\(\overrightarrow{AC}\)を実数倍を図的に足したものとできるんでした。
式にするとこんな感じ。
$$\overrightarrow{AH}=\it{s}\overrightarrow{AB}+\it{t}\overrightarrow{AC}$$
ここから始点をOに揃えて整理すると、以下のようになります。
$$\overrightarrow{OH}=\it\left({1-s-t}\right)\overrightarrow{OA}+\it{s}\overrightarrow{OB}+\it{t}\overrightarrow{OC}$$
ただ、毎回このようにやっていると大変なので、最初からこの結論が出せるようになるまで練習を重ねてくださいね!
後は、先程求めた内積の式に代入し、問題の条件値を使いながら整理すれば以下の連立方程式を立てられます。
\begin{cases} 3s + 2t – 3 = 0 \\ 2s + 3t – 3 = 0 \end{cases}これを解くと、以下のような答えを得ます。
$$s=t=\frac{3}{5}$$
$$\overrightarrow{OH}=-\frac{1}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}+\frac{3}{5}\overrightarrow{c}$$
計算過程は省きましたが、僕がお伝えしたいのは計算方法ではなく、解答の流れです。
4つの条件を上から順に当てはめて式を立てていくという流れを、ぜひ他の問題でも練習してみてくださいね。
以上で演習を終わります。お疲れ様でした!
終わりに
今回は、平面&空間ベクトルの頻出問題を機械的に解くことができる最強の解法をご紹介いたしました。
みなさんいかがだったでしょうか?
まだまだ慣れないところもあるかと思いますが、ベクトルは練習すれば必ずパターンが見えてきます。
理由は、問題を解く上で使う条件がご紹介した4つだけだからです。
ベクトルが苦手な方はぜひ、条件の理解から始めてみてくださいね。
最後に、ここまで見てくださった優秀な皆さんに課題を出そうと思います笑
ぜひ取り組んで見てください!
【課題】京都大
座標空間に4点 A(2,1,0) , B(1,0,1) , C(0,1,2) , D(1,3,7)がある。
3点A,B,Cを通る平面に関して点Dと対称な点をEとするとき、点Eの座標を求めよ。
この問題も今回伝授した解法で解くことができます。
しっかり状況を設定し、図を書きながら解いてみてください!
本問の解答・解説はこちらからどうぞ!

長くなりましたが、今回はここまでにしたいと思います。
お付き合いいただきありがとうございました!